

And so now we're ready toĪpply the product rule. When we just talked about common derivatives. The derivative of g of x is just the derivative Just going to be equal to 2x by the power rule, and
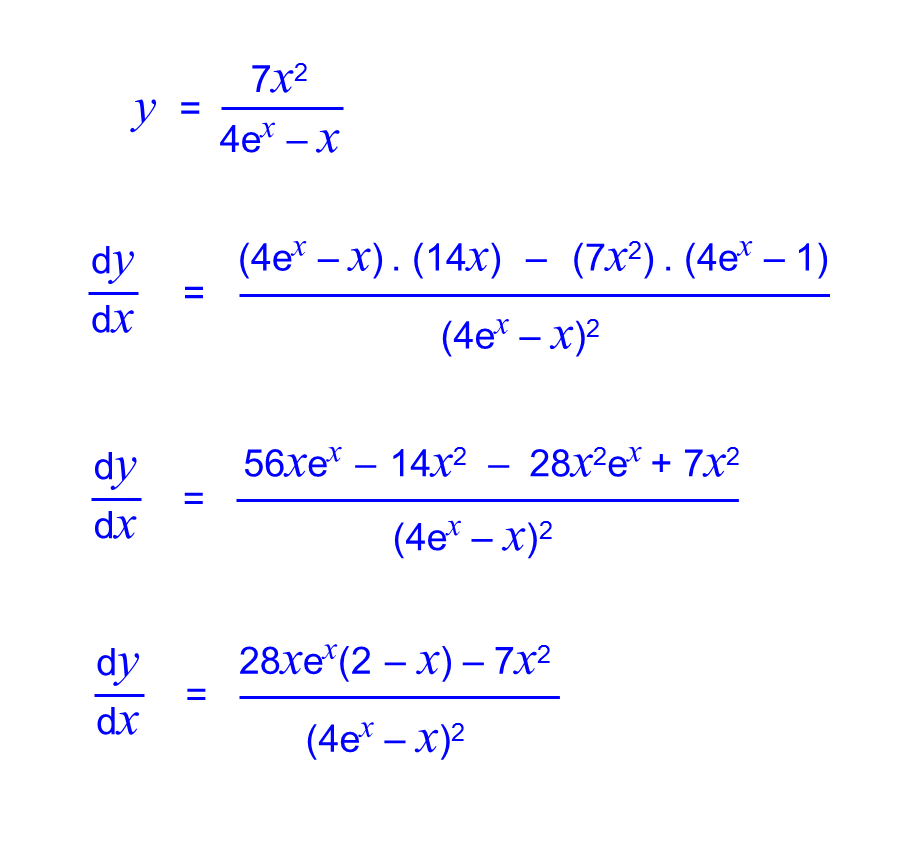
With- I don't know- let's say we're dealing with We derive each rule and demonstrate it with an example. The Quotient Rule For Exponents is the following. Sharing is caringTweetIn this post, we are going to explain the product rule, the chain rule, and the quotient rule for calculating derivatives. Now let's see if we can actuallyĪpply this to actually find the derivative of something. Definition: The Quotient Rule for Exponents For any real number a and positive numbers m and n, where m > n. Times the derivative of the second function. Suppose you have the function y (x + 3)/ (- x 2). The quotient rule is similarly applied to functions where the f and g terms are a quotient. In each term, we tookĭerivative of the first function times the second Here, we want to focus on the economic application of calculus, so well take Newtons word for it that the rules work, memorize a few.
#Quotient rule calculus plus#
Plus the first function, not taking its derivative,

Of the first one times the second function To the derivative of one of these functions, The Quotient Rule says that the derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. Of this function, that it's going to be equal The basic formula for integral calculus is the standard rule for a definite integral: the integral from a to b of f(x) dx is F(b) - F(a) where F is some antiderivative of f. Of two functions- so let's say it can be expressed asį of x times g of x- and we want to take the derivative lim xa f (x) g(x) 0 0 OR lim xa f (x) g(x) lim x a f ( x) g ( x) 0 0 OR lim x a f ( x) g ( x) where a a can be any real number, infinity or negative infinity. Since every quotient can be written as a product, it is always possible to. It is often possible to calculate derivatives in more than one way, as we have already seen. If we have a function that can be expressed as a product d dx x2 + 1 x3 3x 2x(x3 3x) (x2 + 1)(3x2 3) (x3 3x)2 x4 6x2 + 3 (x3 3x)2. Rule, which is one of the fundamental ways Personally, I don't think I would normally do that last stuff, but it is good to recognize that sometimes you will do all of your calculus correctly, but the choices on multiple-choice questions might have some extra algebraic manipulation done to what you found. Combine the differentiation rules to find the derivative of a polynomial or rational function. Extend the power rule to functions with negative exponents. Use the quotient rule for finding the derivative of a quotient of functions. If you are taking AP Calculus, you will sometimes see that answer factored a little more as follows: Use the product rule for finding the derivative of a product of functions. That gets multiplied by the first factor: 18(3x-5)^5(x^2+1)^3. Quotient rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two differentiable. I have mixed feelings about the quotient rule. Now what we're essentially going to do is reapply the product rule to do what many of your calculus books might call the quotient rule. This is hopefully a little bit of review. Now, do that same type of process for the derivative of the second multiplied by the first factor.ĭ/dx = 6(3x-5)^5(3) = 18(3x-5)^5 (Remember that Chain Rule!) So over here is the derivative of f, not of g. That gets multiplied by the second factor: 6x(x^2+1)^2(3x-5)^6 Since every quotient can be written as a product, it is always possible to use the product rule to compute the derivative, though it is not always simpler. Your two factors are (x^2 + 1 )^3 and (3x - 5 )^6 ⇒ f'(x) = \(\mathop \).Remember your product rule: derivative of the first factor times the second, plus derivative of the second factor times the first. To prove quotient rule formula using the definition of derivative or limits, let the function f(x) = u(x)/v(x). Quotient Rule Formula Proof Using Derivative and Limit Properties There are different methods to prove the quotient rule formula, given as, Let us see the proof of the quotient rule formula here. In the previous section, we learned about the quotient formula to find derivatives of the quotient of two differentiable functions.


 0 kommentar(er)
0 kommentar(er)
